eng2beng: A Simple Easy-to-follow Tutorial to a Tiny English to Bengali Machine Translation Model with Transformer Architecture
A 13.25 M parameters, easy-to-understand Transformer-based machine translation model that you can train yourself, inspect, and tinker with. This will help you understand the basic building blocks of language models.
We will use these packages.
pip install torch torchvision torchaudio sentencepiece datasets tqdm sacrebleu
Tokenization
We use a freely available Hugging Face dataset (Hemanth-thunder/english-to-bengali-mt). We want a dataset small enough that is trainable in a few hours, but big enough to learn non-trivial mappings.
For tokenization, we train two separate SentencePiece BPE models — one for English and one for Bengali. Each uses a vocab size of 32,000 tokens.
import io
import sentencepiece as spm
from datasets import load_dataset
dataset = load_dataset("Hemanth-thunder/english-to-bengali-mt", split="train")
#############################################
# Train English tokenizer
en_tokenizer_bio = io.BytesIO()
spm.SentencePieceTrainer.train(
sentence_iterator=iter(dataset['en']),
model_writer=en_tokenizer_bio,
vocab_size=32000,
model_type='bpe',
bos_id=1,
eos_id=2,
pad_id=0,
unk_id=3
)
with open('en_tokenizer.model', 'wb') as f:
f.write(en_tokenizer_bio.getvalue())
# # Directly load the model from serialized model.
# en_tokenizer = spm.SentencePieceProcessor(model_proto=en_tokenizer_bio.getvalue())
en_tokenizer = spm.SentencePieceProcessor()
en_tokenizer.load('en_tokenizer.model')
print(en_tokenizer.encode('this is test'))
#############################################
# Train Bengali tokenizer
bn_tokenizer_bio = io.BytesIO()
spm.SentencePieceTrainer.train(
sentence_iterator=iter(dataset['bn']),
model_writer=bn_tokenizer_bio,
vocab_size=32000,
model_type='bpe',
bos_id=1,
eos_id=2,
pad_id=0,
unk_id=3
)
with open('bn_tokenizer.model', 'wb') as f:
f.write(bn_tokenizer_bio.getvalue())
# # Directly load the model from serialized model.
# bn_tokenizer = spm.SentencePieceProcessor(model_proto=bn_tokenizer_bio.getvalue())
bn_tokenizer = spm.SentencePieceProcessor()
bn_tokenizer.load('bn_tokenizer.model')
print(bn_tokenizer.encode('এটা পরীক্ষা'))
The Dataloader
We use IterableDataset to avoid loading everything into RAM.
from torch.utils.data import IterableDataset, DataLoader
from datasets import load_dataset
import torch
set_seed(52)
class TranslationIterableDataset(IterableDataset):
def __init__(self, split='train', en_tokenizer=None, bn_tokenizer=None, block_size=128):
self.en_tokenizer = en_tokenizer
self.bn_tokenizer = bn_tokenizer
self.block_size = block_size
self.dataset = load_dataset("Hemanth-thunder/english-to-bengali-mt", split=split, streaming=True)
def __iter__(self):
for item in self.dataset:
source_text = item['en']
target_text = item['bn']
source_tokens = self.en_tokenizer.encode(source_text)[:self.block_size - 1] + [2]
target_tokens = [1] + self.bn_tokenizer.encode(target_text)[:self.block_size - 2] + [2]
source_tokens += [0] * (self.block_size - len(source_tokens))
target_tokens += [0] * (self.block_size - len(target_tokens))
yield {
'input_ids': torch.tensor(source_tokens, dtype=torch.long),
'labels': torch.tensor(target_tokens, dtype=torch.long)
}
def collate_fn(batch):
input_ids = torch.stack([item['input_ids'] for item in batch])
labels = torch.stack([item['labels'] for item in batch])
return input_ids, labels
def create_data_loader(split, batch_size, en_tokenizer, bn_tokenizer, block_size=128):
dataset = TranslationIterableDataset(split, en_tokenizer, bn_tokenizer, block_size)
return DataLoader(dataset, batch_size=batch_size, collate_fn=collate_fn)
The Model
The architecture is standard Transformer fare:
- Embedding layers for source and target languages.
- Sinusoidal positional encodings (just like in the paper).
- A PyTorch
nn.Transformermodule handling all the attention and feedforward logic. - A final linear layer to map decoder outputs to vocabulary logits.
This is basically the Transformer architecture distilled to its minimalist essence.
import torch.nn as nn
import math
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=5000):
super().__init__()
self.dropout = nn.Dropout(dropout)
pe = torch.zeros(max_len, d_model)
pos = torch.arange(0, max_len).unsqueeze(1).float()
div = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(pos * div)
pe[:, 1::2] = torch.cos(pos * div)
pe = pe.unsqueeze(1) # [max_len, 1, d_model]
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:x.size(0)]
return self.dropout(x)
class TransformerModel(nn.Module):
def __init__(self, src_vocab_size, tgt_vocab_size, d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward, dropout=0.1):
super().__init__()
self.d_model = d_model
self.src_embed = nn.Embedding(src_vocab_size, d_model, padding_idx=0)
self.tgt_embed = nn.Embedding(tgt_vocab_size, d_model, padding_idx=0)
self.pos_encoder = PositionalEncoding(d_model, dropout)
self.transformer = nn.Transformer(
d_model=d_model,
nhead=nhead,
num_encoder_layers=num_encoder_layers,
num_decoder_layers=num_decoder_layers,
dim_feedforward=dim_feedforward,
dropout=dropout
)
self.fc_out = nn.Linear(d_model, tgt_vocab_size)
def forward(self, src, tgt):
src_mask = None
tgt_mask = nn.Transformer.generate_square_subsequent_mask(tgt.size(0)).to(tgt.device)
src_key_padding_mask = (src == 0).transpose(0, 1)
tgt_key_padding_mask = (tgt == 0).transpose(0, 1)
src = self.src_embed(src) * math.sqrt(self.d_model)
tgt = self.tgt_embed(tgt) * math.sqrt(self.d_model)
src = self.pos_encoder(src)
tgt = self.pos_encoder(tgt)
output = self.transformer(
src,
tgt,
src_mask=src_mask,
tgt_mask=tgt_mask,
src_key_padding_mask=src_key_padding_mask,
tgt_key_padding_mask=tgt_key_padding_mask,
memory_key_padding_mask=src_key_padding_mask
)
return self.fc_out(output)
The Training Setup
Training is standard:
- Loss:
CrossEntropyLoss(ignore_index=0)— we ignore padding. - Optimizer:
AdamW - Decoding: Greedy for now (because beam search would be overkill for our humble model).
We also:
- Shift the target sequence during training (teacher forcing).
- Use a causal mask so that the decoder only sees past tokens.
- Pad all sequences to a fixed length (
block_size = 32).
Here’s the training script.
import torch.optim as optim
from torch.nn.utils import clip_grad_norm_
from tqdm import tqdm
# Hyperparameters
block_size = 32
batch_size = 256
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Model
model = TransformerModel(
src_vocab_size=32000,
tgt_vocab_size=32000,
d_model=128,
nhead=2,
num_encoder_layers=2,
num_decoder_layers=2,
dim_feedforward=512,
dropout=0.1
).to(device)
print(f"Total {sum(p.numel() for p in model.parameters())/1e6} M parameters.")
# Optimizer and loss
optimizer = optim.AdamW(model.parameters(), lr=5e-4)
loss_fn = nn.CrossEntropyLoss(ignore_index=0)
# DataLoader
train_loader = create_data_loader('train', batch_size, en_tokenizer, bn_tokenizer, block_size)
# Training
num_epochs = 10
for epoch in range(num_epochs):
model.train()
total_loss = 0
batch_count = 0
for src_batch, tgt_batch in tqdm(train_loader, desc=f"Epoch {epoch+1}/{num_epochs}"):
src_batch = src_batch.transpose(0, 1).to(device) # [seq_len, batch_size]
tgt_batch = tgt_batch.transpose(0, 1).to(device)
optimizer.zero_grad()
output = model(src_batch, tgt_batch[:-1]) # decoder input (exclude last token)
loss = loss_fn(output.view(-1, output.size(-1)), tgt_batch[1:].reshape(-1)) # target shifted
loss.backward()
clip_grad_norm_(model.parameters(), max_norm=1.0)
optimizer.step()
total_loss += loss.item()
batch_count += 1
print(f"Epoch {epoch+1}: Loss = {total_loss / batch_count:.4f}")
save_model(model, 'eng2beng_0_2_1_epoch_10.pt')
After 10 epochs, the model lands at a loss of around 3.89 — not bad for such a small network trained on limited data.
Inference
Here is the inference script.
# Inference
PAD_ID = 0
BOS_ID = 1
EOS_ID = 2
MAX_LENGTH = 32
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
@torch.no_grad()
def translate(sentence):
model.eval()
# Encode English sentence and add <eos>
src_tokens = en_tokenizer.encode(sentence)[:MAX_LENGTH - 1] + [EOS_ID]
src_tensor = torch.tensor(src_tokens, dtype=torch.long).unsqueeze(1).to(DEVICE) # [seq_len, 1]
# Encoder padding mask
src_key_padding_mask = (src_tensor == PAD_ID).transpose(0, 1) # [1, seq_len]
# Encode once
src_emb = model.src_embed(src_tensor) * (model.d_model ** 0.5)
src_emb = model.pos_encoder(src_emb)
memory = model.transformer.encoder(src_emb, src_key_padding_mask=src_key_padding_mask)
# Initialize decoder input with <sos>
generated = [BOS_ID]
for _ in range(MAX_LENGTH):
tgt_tensor = torch.tensor(generated, dtype=torch.long).unsqueeze(1).to(DEVICE) # [tgt_seq_len, 1]
tgt_emb = model.tgt_embed(tgt_tensor) * (model.d_model ** 0.5)
tgt_emb = model.pos_encoder(tgt_emb)
tgt_mask = nn.Transformer.generate_square_subsequent_mask(tgt_tensor.size(0)).to(DEVICE)
output = model.transformer.decoder(
tgt=tgt_emb,
memory=memory,
tgt_mask=tgt_mask,
memory_key_padding_mask=src_key_padding_mask
)
logits = model.fc_out(output) # [tgt_seq_len, 1, vocab_size]
next_token_logits = logits[-1, 0] # last time step
next_token_id = next_token_logits.argmax().item()
if next_token_id == EOS_ID:
break
generated.append(next_token_id)
# Decode Bengali tokens
return bn_tokenizer.decode(generated[1:]) # Skip <sos>
Samples
Here are few generated samples.
print(translate("He is a good boy."))
print(translate("What is her name?"))
print(translate("I am very hungry."))
print(translate("I am very angry."))
print(translate("He will return next week."))
print(translate("I am going to the market. I will buy some vegetables."))
print(translate("i am here."))
print(translate("where is the mall?"))
print(translate("what should we do?"))
print(translate("today what should we do?"))
print(translate("what's the word on the street?"))
print(translate("I am going to the cinema."))
print(translate("what is the meaning of life?"))
print(translate("The artist is painting a beautiful picture."))
print(translate("She is preparing our lunch."))
তিনি একজন ভাল ছেলে।
তার নাম কী?
আমি খুব ক্ষুধার্ত।
আমি খুব রেগে আছি।
পরের সপ্তাহে তিনি ফিরে আসবেন।
আমি শাকসবজি কিনতে যাচ্ছি।
আমি এখানে এসেছি।
কোথায় শপিং মল?
আমরা কী করব?
আজ আমরা কী করব?
রাস্তার রাস্তার উপর কী?
আমি সিনেমাটি সিনেমাতে যাচ্ছি।
জীবনের অর্থ কী?
চিত্রশিল্পের একটি সুন্দর চিত্র।
তিনি আমাদের দুপুরের খাবার প্রস্তুত।
Evaluation: BLEU Score
We use sacrebleu for evaluation. It’s standard, robust, and tells us how close we are to human-like translations. We achieve a score of 11.60 on a completely new dataset(not held-out test data from the same dataset). Here’s the evaluation function.
import sacrebleu
import pandas as pd
@torch.no_grad()
def evaluate_bleu(df_eval, model, tokenizer_en, tokenizer_bn, device, max_len=96):
model.eval()
preds = []
refs = []
for idx, row in tqdm(df_eval.iterrows()):
src_text = row['en']
ref_text = row['bn']
# Encode source
src_tokens = tokenizer_en.encode(src_text)
src_tensor = torch.tensor(src_tokens, dtype=torch.long).unsqueeze(1).to(device) # (seq_len, batch)
# Encoder padding mask
src_key_padding_mask = (src_tensor == PAD_ID).transpose(0, 1) # [1, seq_len]
# Encode once
src_emb = model.src_embed(src_tensor) * (model.d_model ** 0.5)
src_emb = model.pos_encoder(src_emb)
memory = model.transformer.encoder(src_emb, src_key_padding_mask=src_key_padding_mask)
# Initialize decoder input with <sos>
generated = [BOS_ID]
for _ in range(MAX_LENGTH):
tgt_tensor = torch.tensor(generated, dtype=torch.long).unsqueeze(1).to(DEVICE) # [tgt_seq_len, 1]
tgt_emb = model.tgt_embed(tgt_tensor) * (model.d_model ** 0.5)
tgt_emb = model.pos_encoder(tgt_emb)
tgt_mask = nn.Transformer.generate_square_subsequent_mask(tgt_tensor.size(0)).to(DEVICE)
output = model.transformer.decoder(
tgt=tgt_emb,
memory=memory,
tgt_mask=tgt_mask,
memory_key_padding_mask=src_key_padding_mask
)
logits = model.fc_out(output) # [tgt_seq_len, 1, vocab_size]
next_token_logits = logits[-1, 0] # last time step
next_token_id = next_token_logits.argmax().item()
if next_token_id == EOS_ID:
break
generated.append(next_token_id)
# Decode predicted tokens
pred_sentence = tokenizer_bn.decode(generated[1:]) # exclude BOS
preds.append(pred_sentence)
refs.append([ref_text]) # list of references for sacrebleu
bleu = sacrebleu.corpus_bleu(preds, refs)
print(f"BLEU Score: {bleu.score:.2f}")
return preds, bleu.score
For simple sentences, the model performs decently. Complex sentences? That’s where it struggles — but again, this is a baby Transformer. Just tuning the model dimension hyperparameters like d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward etc. and maybe implementing a learnable positional embedding (like in BERT, GPT) (which is also a nice next step) would produce magic!
Here’s a link to the github repo that contains the notebook and the tokenizers.
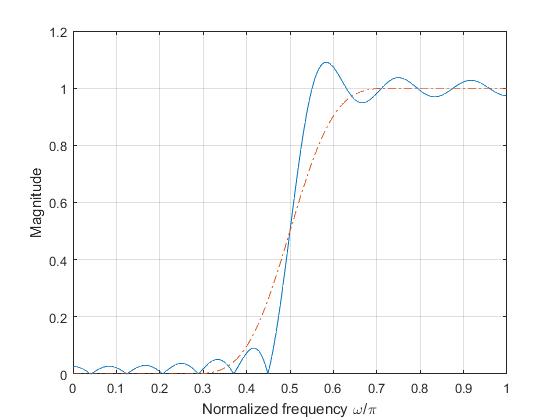
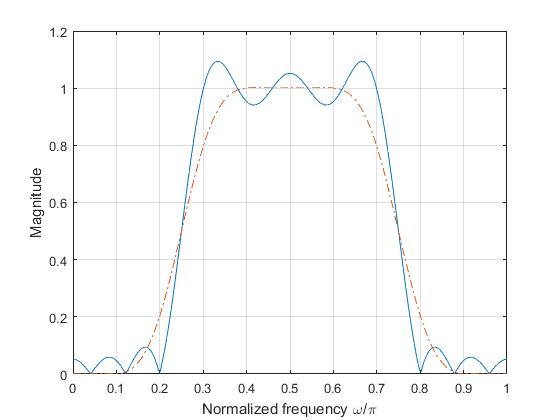
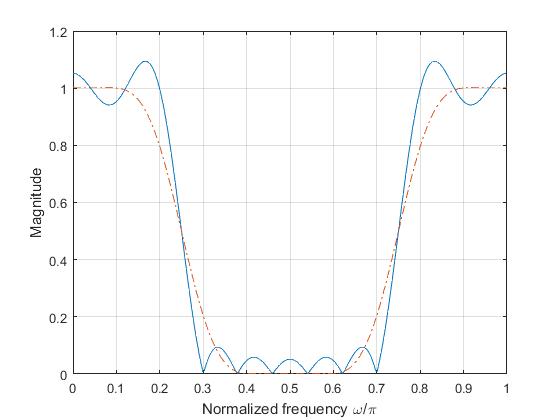
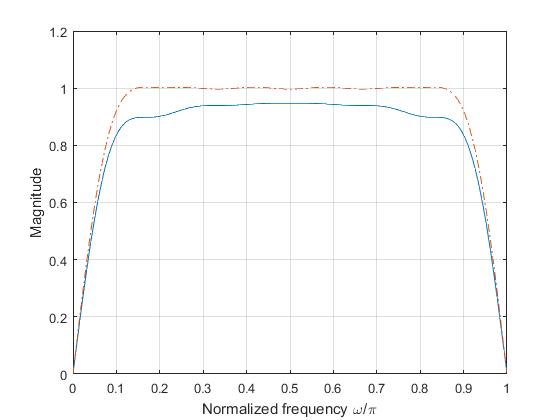
where \(\beta =^{def} \pi\alpha\).
The coefficients of a Kaiser window are computed from the following equation:
\[w(n) = \frac{I_0\left(\beta\sqrt{1 - \left(\frac{n - N/2}{N/2}\right)^2}\right)}{I_0(\beta)}, \qquad 0 \le n \le N\]
where \(I_0\) is the zeroth-order modified Bessel function of the first kind. The length \(L = N + 1\).
