A link to the previous part, a link to the first part and a link to the references part.

25-tap Lowpass Filter using Rectangular and Hamming Windows

The rectwin and hamming functions create the rectangular and Hamming window.

Rectangular window from wikimedia Hamming window from wikimedia

The Hamming window is generated from the equation: \[w(n) = 0.54 - 0.46 cos\left(2\pi\frac{n}{N}\right), \qquad 0 \le n \le N\] The window length \(L = N + 1\).

%% To design a 25-tap lowpass filter with cutoff frequency .5pi radians
% using rectangular and Hamming windows and plot their frequency response
wc = .5*pi;      % Cutoff frequency
N = 25; alpha = (N-1)/2; eps = .001;
n = 0:1:N-1;
hd = sin(wc*(n-alpha+eps))./(pi*(n-alpha+eps));
wr = rectwin(N); % Rectangular window sequence
hn = hd.*wr';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h)); hold on
wh = hamming(N); % Hamming window sequence
hn = hd.*wh';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

Frequency response of 25-tap lowpass filter using rectangular and Hamming windows

25-tap Highpass Filter using Rectangular and Blackman Windows

The blackman function creates the Blackman window.

Blackman window from wikimedia

The following equation defines the Blackman window of length \(N\): \[w(n) = 0.42 - 0.5 cos\frac{2\pi n}{N - 1} + 0.08cos\frac{4\pi n}{N - 1}, \] \[0 \le n \le M - 1\] where \(M\) is \(N/2\) for \(N\) even and \((N + 1)/2\) for \(N\) odd.

%% To design a 25-tap highpass filter with cutoff frequency .5pi radians
% using rectangular and Blackman windows and plot their frequency response
wc = .5*pi;      % Cutoff frequency
N = 25; alpha = (N-1)/2; eps = .001;
n = 0:1:N-1;
hd = (sin(pi*(n-alpha+eps)) - sin(wc*(n-alpha+eps))) ./ (pi*(n-alpha+eps));
wr = rectwin(N); % Rectangular window sequence
hn = hd.*wr';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h)); hold on
wh = blackman(N); % Blackman window sequence
hn = hd.*wh';     % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

Frequency response of 25-tap highpass filter using rectangular and Blackman windows

25-tap Bandpass Filter using Rectangular and Hamming Windows

%% To design a 25-tap bandpass filter with cutoff frequency .25pi and .75pi radians
% using rectangular and Hamming windows and plot their frequency response
wc1 = .25*pi; wc2 = .75*pi;      % Cutoff frequency
N = 25; a = (N-1)/2;
eps = .001; % To avoid indeterminate form
n = 0:1:N-1;
hd = (sin(wc2*(n-a+eps)) - sin(wc1*(n-a+eps))) ./ (pi*(n-a+eps));
wr = rectwin(N); % Rectangular window sequence
hn = hd.*wr';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h)); hold on
wh = hamming(N); % Hamming window sequence
hn = hd.*wh'; % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

Frequency response of 25-tap bandpass filter using rectangular and Hamming windows

25-tap Bandstop Filter using Rectangular and Hamming Windows

%% To design a 25-tap bandstop filter with cutoff frequency .25pi and .75pi radians
% using rectangular and Hamming windows and plot their frequency response
wc1 = .25*pi; wc2 = .75*pi;      % Cutoff frequency
N = 25; a = (N-1)/2;
eps = .001; % To avoid indeterminate form
n = 0:1:N-1;
hd = (sin(wc1*(n-a+eps)) - sin(wc2*(n-a+eps)) + sin(pi*(n-a+eps))) ./ (pi*(n-a+eps));
wr = rectwin(N); % Rectangular window sequence
hn = hd.*wr';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h)); hold on
wh = hamming(N); % Hamming window sequence
hn = hd.*wh';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

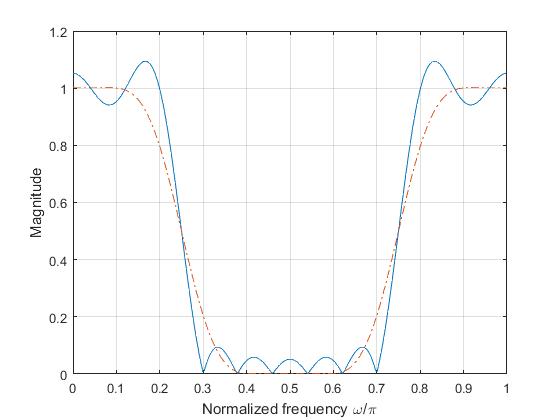
Frequency response of 25-tap bandstop filter using rectangular and Hamming windows

25-tap Hilbert Transformer using Bartlett and Hamming Windows

Triangular window from wikimedia

The coefficients of a Bartlett window are computed as follows: \[w(n) = \begin{cases} \frac{2n}{N}, & \text{\(0 \le n \le \frac{N}{2}\)} \\[2ex] 2-\frac{2n}{N}, & \text{\(\frac{N}{2} \le n \le N\)} \end{cases} \] The window length \(L = N + 1\).

%% To design a 25-tap Hilbert transformer using Bartlett
%  and Hamming windows and plot their frequency response
N = 25; a = (N-1)/2; eps = .001;
n = 0:1:N-1;
hd = (1 - cos(pi*(n-a+eps))) ./ (pi*(n-a+eps)); hd(a+1) = 0;
wt = bartlett(N); % Bartlett window
hn = hd.*wt';     % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h));   hold on
wh = hamming(N); % Hamming window sequence
hn = hd.*wh';    % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

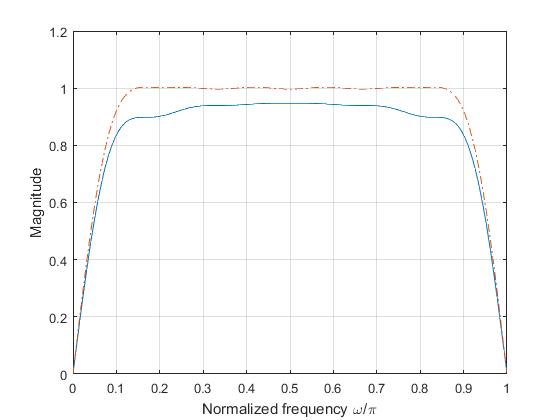
Frequency response of 25-tap Hilbert transformer using Bartlett and Hamming windows

25-tap Differentiator using Rectangular, Bartlett and Hann Windows

Hann window from wikimedia

The following equation generates the coefficients of a Hanning window: \[w(n) = 0.5\left(1−cos\left(2\pi\frac{n}{N}\right)\right), \qquad 0 \le n \le N\] The window length \(L = N + 1\).

%% To design a 25-tap differentiator using rectangular, Bartlett
%  and Hanning windows and plot their frequency response
N = 25; a = (N-1)/2; eps = .001;
n = 0:1:N-1;
hd = cos(pi*(n-a)) ./ (pi*(n-a)); hd(a+1) = 0;
wr = rectwin(N);  % rectangular window
hn = hd.*wr';     % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-.'); hold on
wt = bartlett(N); % Bartlett window
hn = hd.*wt';     % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'--'); hold on
wh = hann(N); % Hanning window sequence
hn = hd.*wh'; % Filter coefficients
w = 0:.01:pi;
h = freqz(hn,1,w);
plot(w/pi,abs(h),'-');  grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude');    hold off

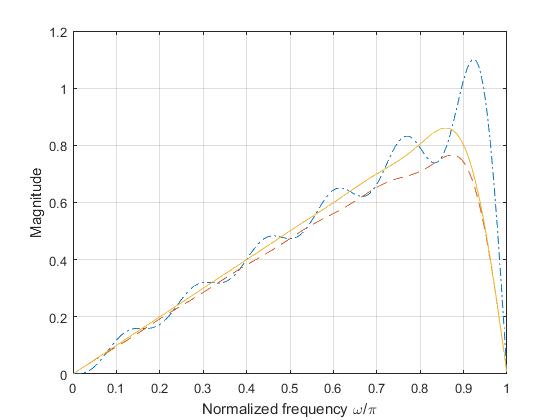
Frequency response of 25-tap differentiator using rectangular, Bartlett and Hanning windows

FIR Lowpass Filter using Hamming and Blackman Windows

The following equation defines the Blackman window of length N: \[w(n) = 0.42 − 0.5 cos\frac{2\pi n}{N - 1} + 0.08 cos\frac{4\pi n}{N - 1}, \] \[0 \le n \le M - 1\] where \(M\) is \(N/2 \) for \(N\) even and \((N + 1)/2 \) for \(N\) odd.

%% To design an FIR lowpass filter using Hamming and Blackman windows
wc = 0.5*pi; % Cutoff frequency
N = 25;
b = fir1(N,wc/pi,hamming(N+1));
w = 0:.01:pi;
h = freqz(b,1,w);
plot(w/pi,abs(h));   hold on
b = fir1(N,wc/pi,blackman(N+1));
w = 0:.01:pi;
h = freqz(b,1,w);
plot(w/pi,abs(h),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude'); hold off

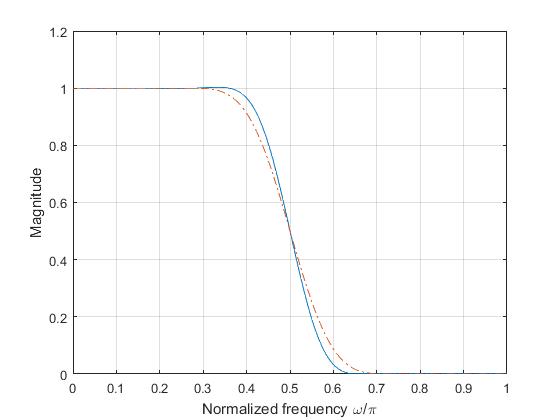
FIR lowpass filter using Hamming and Blackman windows

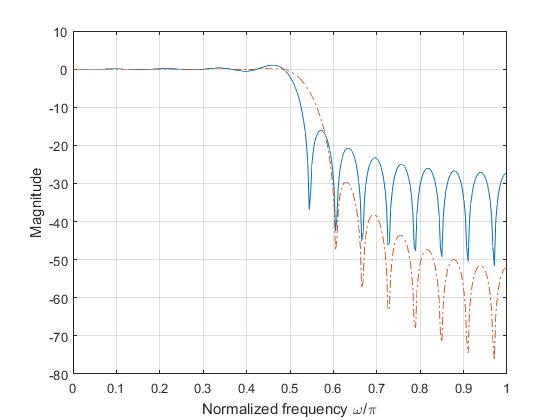
Lowpass Filter using Kaiser Window

Kaiser window from wikimedia where \(\beta =^{def} \pi\alpha\). The coefficients of a Kaiser window are computed from the following equation: \[w(n) = \frac{I_0\left(\beta\sqrt{1 - \left(\frac{n - N/2}{N/2}\right)^2}\right)}{I_0(\beta)}, \qquad 0 \le n \le N\] where \(I_0\) is the zeroth-order modified Bessel function of the first kind. The length \(L = N + 1\).

%% To plot the frequency response of lowpass filter using Kaiser window
%  for different values of beta
wc = 0.5*pi; % Cutoff frequency
N = 25;
b = fir1(N,wc/pi,kaiser(N+1,.5));   %Beta = .5
w = 0:.01:pi;
h = freqz(b,1,w);
plot(w/pi,20*log10(abs(h)));      hold on
b = fir1(N,wc/pi,kaiser(N+1,3.5));  %Beta = 3.5
w = 0:.01:pi;
h = freqz(b,1,w);
plot(w/pi,20*log10(abs(h)),'-.'); hold on
b = fir1(N,wc/pi,kaiser(N+1,8.5));  %Beta = 8.5
w = 0:.01:pi;
h = freqz(b,1,w);
plot(w/pi,20*log10(abs(h)),'--'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude');              hold off

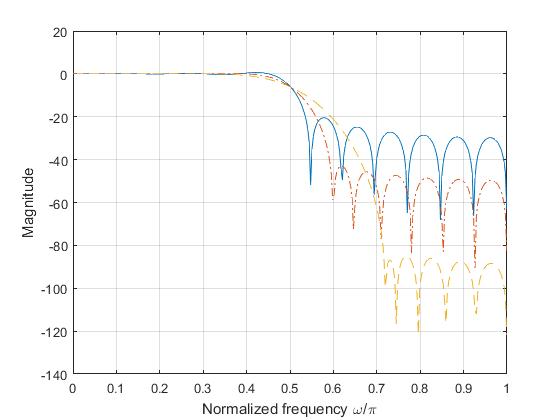
Frequency response of lowpass filter using Kaiser window

FIR Lowpass Filter using Frequency Sampling Method

%% To design a FIR lowpass filter with cutoff frequency .5pi using frequency sampling method
N = 33; % Number of samples
alpha = (N-1)/2;
Hrk = [ones(1,9), zeros(1,16), ones(1,8)]; % Samples of magnitude response
k1 = 0:(N-1)/2; k2 = (N+1)/2:N-1;
theta_k = [(-alpha*(2*pi)/N)*k1,(alpha*(2*pi)/N)*(N-k2)];
Hk = Hrk.*(exp(1i*theta_k));
hn = real(ifft(Hk,N));
w = 0:.01:pi;
H = freqz(hn,1,w);
plot(w/pi,20*log10(abs(H))); hold on
% FIR filter design using frequency sampling method with a transition sample
% at Hk(9) = 0.5 and Hk(24) = 0.5
Hrk = [ones(1,9), 0.5, zeros(1,14), 0.5, ones(1,8)]; % Samples of magnitude response
k1 = 0:(N-1)/2; k2 = (N+1)/2:N-1;
theta_k = [(-alpha*(2*pi)/N)*k1, (alpha*(2*pi)/N)*(N-k2)];
Hk = Hrk.*(exp(1i*theta_k));
hn = real(ifft(Hk,N));
w = 0:.01:pi;
H = freqz(hn,1,w);
plot(w/pi,20*log10(abs(H)),'-.'); grid;
xlabel('Normalized frequency \omega/\pi');
ylabel('Magnitude');         hold off

FIR lowpass filter using frequency sampling method

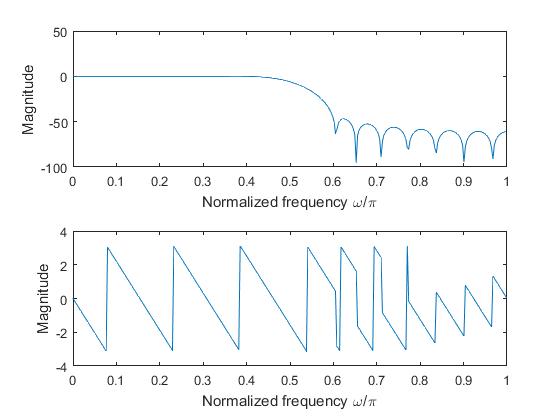
FIR Lowpass Filter using Kaiser Window

%% To design an FIR lowpass filter for the given specifications using Kaiser window
alphap = 0.1; % Passband attenuation in dB
alphas = 44;  % Stopband attenuation in dB
ws = 30;      % Stopband frequency in rad/sec
wp = 20;      % Passband frequency in rad/sec
wsf = 100;    % Sampling frequency in rad/sec
B = ws - wp;  % Transition width
wc = 0.5*(ws+wp);  % Cutoff frequency in rad/sec
wcr = wc*2*pi/wsf; % Cutoff drequenct=y in rad
D = (alphas - 7.95) / 14.36;
N = ceil((wsf*D/B)+1); % Order of the filter
alpha = (N-1) / 2
gamma = (.5842*(alphas-21).^(0.4)+0.07886*(alphas-21));
n = 0:1:N-1;
hd = sin(wcr*(n-alpha)) ./ (pi*(n-alpha)); hd(alpha+1) = 0.5;
wk = (kaiser(N,gamma))';
hn = hd.*wk;
w = 0:.01:pi;
h = freqz(hn,1,w);
subplot(2,1,1), plot(w/pi,20*log10(abs(h)))
xlabel('Normalized frequency \omega/\pi'); ylabel('Magnitude');
subplot(2,1,2), plot(w/pi,angle(h))
xlabel('Normalized frequency \omega/\pi'); ylabel('Magnitude');

FIR lowpass filter using Kaiser window

This repo contains all the scripts used in this post. Here is a link to the previous part, a link to the first part and a link to the references part.