A link to the previous part, a link to the next part and a link to the references part.
DFT of a Sequence - Magnitude and Phase Response
The function takes the input sequence and the number of frequency points as two arguments.
%% DFT of a sequence and plot of the magnitude and phase response
x = ones(1,4); %Input sequence
N1 = 8; %Number of frequency points
Y1 = dft(x,N1)
k = 0:1:N1-1;
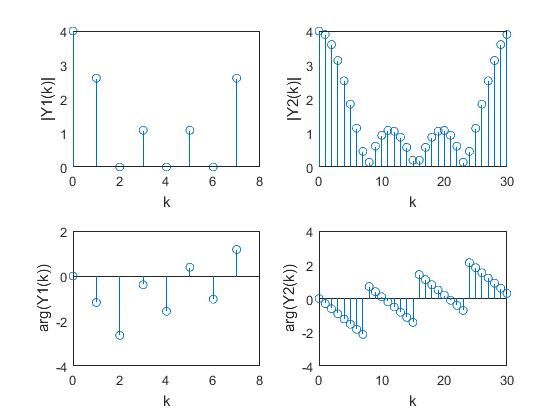
subplot(2,2,1), stem(k,abs(Y1)), xlabel('k'), ylabel('|Y1(k)|');
subplot(2,2,3), stem(k,angle(Y1)), xlabel('k'), ylabel('arg(Y1(k))');
N2 = 31 %Number of frequency points
Y2 = dft(x,N2)
k = 0:1:N2-1;
subplot(2,2,2), stem(k,abs(Y2)), xlabel('k'), ylabel('|Y2(k)|');
subplot(2,2,4), stem(k,angle(Y2)), xlabel('k'), ylabel('arg(Y2(k))');
dft.m:
function X = dft(xn,N)
% To compute the DFT of the sequence x(n)
L = length(xn); %Length of the sequence
%Checking for the length of the DFT
if(N<L)
error('N must be >=L')
end
x1 = [xn zeros(1,N-L)]; %Appending zeros
%Computation of twiddle factors
for k = 0:1:N-1
for n = 0:1:N-1
p = exp(-i*2*pi*n*k/N);
x2(k+1,n+1) = p;
end
end
X = x1 * x2;
Notice that the Command Window shows the two output sequences of the 8-point and 50-point DFT.
Inverse DFT of a Sequence
%% Inverse DFT of a sequence
X = [4,1+i,0,1,-i,0,1+i,1-i];
N = length(X);
xn = idft(X,N)
idft.m:
function xn = idft(X,N)
%To compute the inverse DFT of the sequence X(k)
L = length(X); %Length of the sequence
%Computation of twiddle factors
for k = 0:1:N-1
for n = 0:1:N-1
p = exp(i*2*pi*n*k/N);
x2(k+1,n+1) = p;
end
end
xn = (X*x2.')/N;
Command Window output:
xn =
Columns 1 through 7
1.0000 + 0.0000i 0.5366 + 0.0884i 0.1250 - 0.3750i 0.1098 + 0.3384i 0.2500 + 0.0000i 0.7134 - 0.0884i 0.6250 - 0.1250i
Column 8
0.6402 + 0.1616i
Circular Convolution of two Sequences
%% Circular convolution of two sequences
n = 0:7;
x = sin(3*pi*n/8); % Input sequence 1
h = [1,1,1,1]; % Input sequence 2
Nx = length(x);
Nh = length(h);
N = 8;
if(N<max(Nx,Nh))
error('N must be >=max(Nx,Nh')
end
y = circconv(x,h,N)
circconv.m:
function [y] = circconv(x,h,N);
% To find the circular convolution of two sequences
% x = input sequence 1
% h = impulse sequence 2
% N = Number of points in the output sequence
N2 = length(x);
N3 = length(h);
x = [x zeros(1,N-N2)] %Append N-N2 zeros to the input sequence 1
h = [h zeros(1,N-N3)] %Append N-N3 zeros to the sequence 2
% circular shift of the sequence 2
m = [0:1:N-1];
M = mod(-m,N);
h = h(M+1);
for n = 1:1:N
m = n-1;
p = 0:1:N-1;
q = mod(p-m,N);
hm = h(q+1);
H(n,:) = hm;
end
% Matrix convolution
y = x*H';
Command Window output:
x =
0 0.9239 0.7071 -0.3827 -1.0000 -0.3827 0.7071 0.9239
h =
1 1 1 1 0 0 0 0
y =
1.2483 2.5549 2.5549 1.2483 0.2483 -1.0583 -1.0583 0.2483
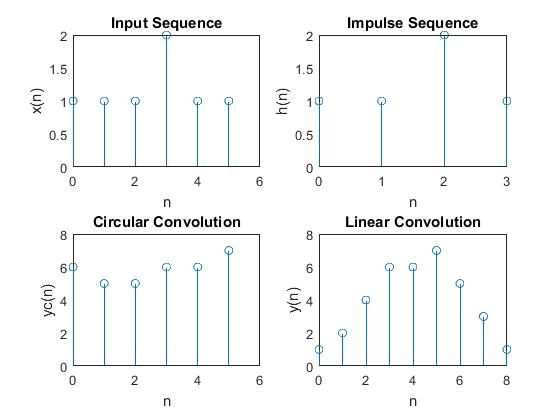
Comparison between Circular and Linear Convolutions of two Sequences
%% Frequency response of given systems
b = [1,0,.9]; %Numerator coefficients of system1
a = [1,0,.4]; %Denominator coefficients of system1
d = [1,-1]; %Numerator coefficients of system2
f = [1,.25]; %Denominator coefficients of system2
w = 0:.01:pi;
[h1] = freqz(b,a,w);
[h2] = freqz(d,f,w);
subplot(2,2,1), plot(w/pi,abs(h1));
xlabel('Normalized frequency \omega/\pi'), ylabel('Magnitide');grid
subplot(2,2,3), plot(w/pi,angle(h1));
xlabel('Normalized fequency \omega/\pi'), ylabel('Phase in radians');grid
subplot(2,2,2), plot(w/pi,abs(h2));
xlabel('Normalized frequency \omega/\pi'), ylabel('Magnitide');grid
subplot(2,2,4), plot(w/pi,angle(h2));
xlabel('Normalized fequency \omega/\pi'), ylabel('Phase in radians');grid
Overlap and Save Method
%% Overlap and save method
x = [1,2,-1,2,3,-2,-3,-1,1,1,2,-1]; % Input sequence
h = [1,2,1,1]; % Impulse sequence
N = 4; % Length of each block before appending zeros
y = ovrlsav(x,h,N);
ovrlsav.m:
function y = ovrlsav(x,h,N)
% To compute the output of a system using overlap and save method
% x = input seuence
% h = impulse sequence
% N = Length of each block
if(N<length(h))
error('N must be >=length(h)')
end
Nx = length(x);
M = length(h);
M1 = M-1;
L = N-M1;
x = [zeros(1,M-1),x,zeros(1,N-1)];
h = [h zeros(1,N-M)];
K = floor((Nx+M1-1)/(L)); % Number of blocks
Y = zeros(K+1,N);
%Dividing the sequence into two blocks
for k = 0:K
xk = x(k*L+1:k*L+N);
Y(k+1,:) = circconv(xk,h,N);
end
Y = Y(:,M:N)'; %Discard first M-1 blocks
y = (Y(:))'
Command Window output:
y =
1 4 4 3 8 5 -2 -6 -6 -1 4 5 1 1 -1
Overlap and Add Method
%% Overlap and add method
x = [1,2,-1,2,3,-2,-3,-1,1,1,2,-1]; %Input sequence
h = [1,2,1,1]; %Impulse sequence
L = 4; %Length of each block before appending zeros
y = ovrladd(x,h,L);
ovrladd.m:
function y = ovrladd(x,h,L)
% To compute the output of a system using overlap and add method
% x = input sequence
% h = impulse sequence
% L = Length of each block
Nx = length(x);
M = length(h);
M1 = M-1;
R = rem(Nx,L);
N = L+M1;
x = [x zeros(1,L-R)];
h = [h zeros(1,N-M)];
K = floor(Nx/L); % Number of blocks
Y = zeros(K+1,N);
z = zeros(1,M1);
% Dividing the sequence into K blocks
for k = 0:K
xp = x(k*L+1:k*L+L);
xk = [xp z];
y(k+1,:) = circconv(xk,h,N);
end
yp = y';
[x,y] = size(yp);
for i = L+1:x
for j=1:y-1
temp1 = i-L;
temp2 = j+1;
temp3 = yp(temp1,temp2)+yp(i,j);
yp(temp1,temp2) = yp(i,j);
yp(temp1,temp2) = temp3;
end
end
z = 1;
for j = 1:y
for i = 1:x
if((i<=L && j<=y-1)||(j==y))
ypnew(z) = yp(i,j);
z = z+1;
end
end
end
y = ypnew
Command Window output:
y =
1 4 4 3 8 5 -2 -6 -6 -1 4 5 1 1 -1 0 0 0 0
Butterworth Lowpass Filter
The buttord and butter functions can be used while designing a Butterworth filter.
%% To design a Butterworth lowpass filter for the specifications
alphap = .4; %Passband attenuation in dB
alphas = 30; %Stopband attenuation in dB
fp = 400; %Passband frequency in Hz
fs = 800; %Stopband frequency in Hz
F = 2000; %Sampling frequency in Hz
omp = 2*fp/F;
oms = 2*fs/F;
%To find cutoff frequency and order of the filter
[n,wn] = buttord(omp,oms,alphap,alphas);
%system function of the filter
[b,a] = butter(n,wn)
w = 0:.01:pi;
[h,om] = freqz(b,a,w,'whole');
m = abs(h);
an = angle(h);
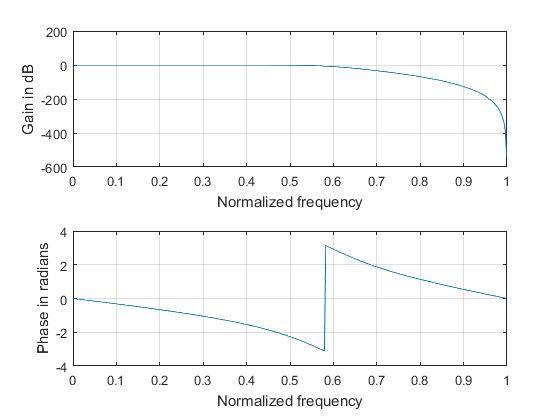
subplot(2,1,1); plot(om/pi,20*log(m)); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(om/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.1518 0.6073 0.9109 0.6073 0.1518
a =
1.0000 0.6418 0.6165 0.1449 0.0259
Butterworth Bandpass Filter
%% To design a Butterworth bandpass filter for the specifications
alphap = 2; %Pass band attenuation in dB
alphas = 20; %Stop band attenuation in dB
wp = [.2*pi,.4*pi]; %Passband frequency in radians
ws = [.1*pi,.5*pi]; %Stopband frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = buttord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = butter(n,wn)
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = 20*log10(abs(h));
an = angle(h);
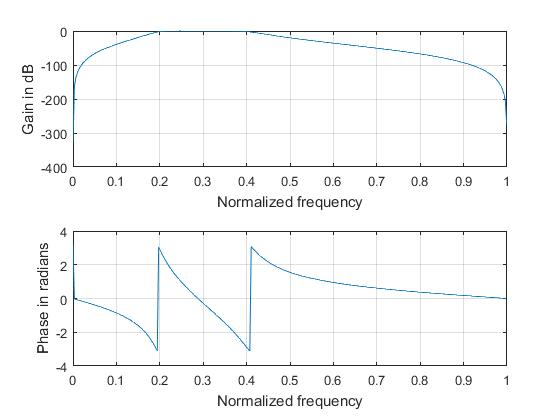
subplot(2,1,1); plot(ph/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.0060 0 -0.0240 0 0.0359 0 -0.0240 0 0.0060
a =
1.0000 -3.8710 7.9699 -10.6417 10.0781 -6.8167 3.2579 -1.0044 0.1670
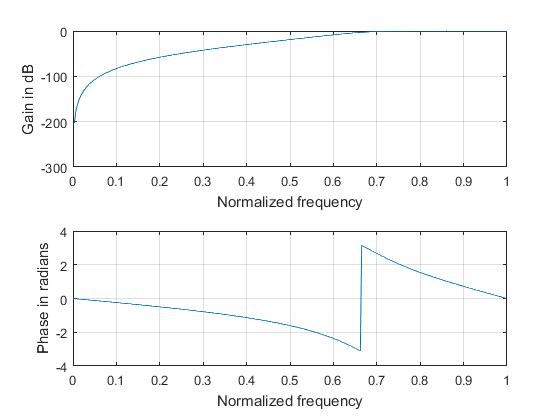
Butterworth Highpass Filter
%% To design a Butterworth highpass filter for the specifications
alphap = .4; % Pass band attenuation in dB
alphas = 30; % Stop band attenuation in dB
fp = 800; % Passband frequency in radians
fs = 400; % Stopband frequency in radians
F = 2000; % Sampling frequency in Hz
omp = 2*fp/F;
oms = 2*fs/F;
%To find cutoff frequency and order of the filter
[n,wn] = buttord(omp,oms,alphap,alphas);
%system function of the filter
[b,a] = butter(n,wn,'high')
w = 0:.01:pi;
[h,om] = freqz(b,a,w);
m = 20*log10(abs(h));
an = angle(h);
subplot(2,1,1); plot(om/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(om/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.0265 -0.1058 0.1587 -0.1058 0.0265
a =
1.0000 1.2948 1.0206 0.3575 0.0550
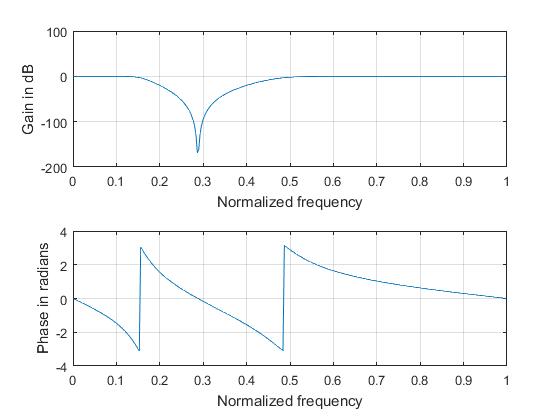
Butterworth Band-stop Filter
%% To design a Butterworth bandstop filter for the specifications
alphap = 2; % Pass band attenuation in dB
alphas = 20; % Stop band attenuation in dB
ws = [.2*pi,.4*pi]; % Stopband frequency in radians
wp = [.1*pi,.5*pi]; % Passband frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = buttord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = butter(n,wn,'stop')
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = 20*log10(abs(h));
an = angle(h);
subplot(2,1,1); plot(ph/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.2348 -1.1611 3.0921 -5.2573 6.2629 -5.2573 3.0921 -1.1611 0.2348
a =
1.0000 -3.2803 5.4917 -6.1419 5.0690 -3.0524 1.3002 -0.3622 0.0558
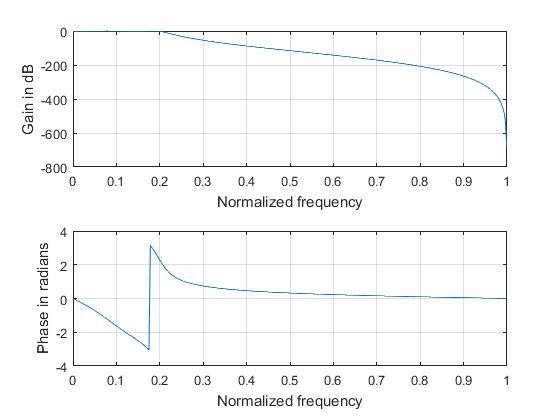
Chebyshev Type I Lowpass Filter
Likewise, the cheb1ord and cheby1 functions can be used while designing a Chebyshev type I filter.
%% To design a Chebyshev 1 lowpass filter for the specifications
alphap = 1; %Pass band attenuation in dB
alphas = 15; %Stop band attenuation in dB
wp = .2*pi; %Pass band frequency in radians
ws = .3*pi; %Stop band frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = cheb1ord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = cheby1(n,alphap,wn)
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = 20*log(abs(h));
an = angle(h);
subplot(2,1,1); plot(ph/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.0018 0.0073 0.0110 0.0073 0.0018
a =
1.0000 -3.0543 3.8290 -2.2925 0.5507
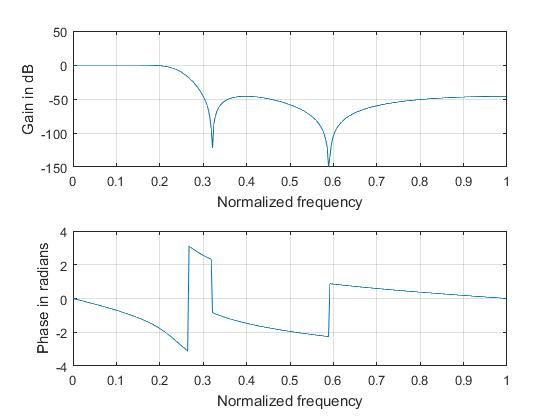
Chebyshev Type II Lowpass Filter
Here cheb2ord and cheby2 are used.
%% To design a Chebyshev 2 lowpass filter for the specifications
alphap = 1; %Pass band attenuation in dB
alphas = 20; %Stop band attenuation in dB
wp = .2*pi; %Pass band frequency in radians
ws = .3*pi; %Stop band frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = cheb2ord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = cheby2(n,alphas,wn)
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = abs(h);
an = angle(h);
subplot(2,1,1); plot(ph/pi,20*log(m)); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.1160 -0.0591 0.1630 -0.0591 0.1160
a =
1.0000 -1.8076 1.5891 -0.6201 0.1153
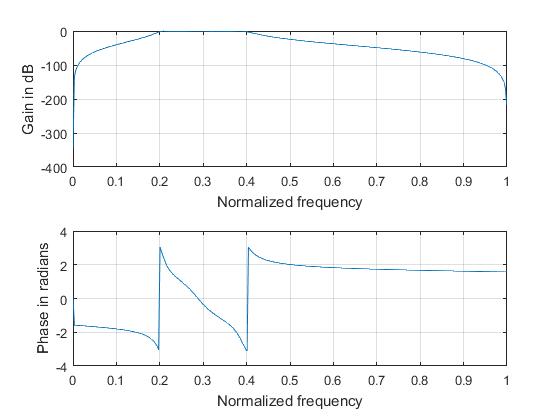
Chebyshev Type I Bandpass Filter
%% To design a Chebyshev 1 bandpass filter for the specifications
alphap = 2; %Pass band attenuation in dB
alphas = 20; %Stop band attenuation in dB
wp = [.2*pi,.4*pi]; %Pass band frequency in radians
ws = [.1*pi,.5*pi]; %Stop band frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = cheb1ord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = cheby1(n,alphap,wn)
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = 20*log10(abs(h));
an = angle(h);
subplot(2,1,1); plot(ph/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.0083 0 -0.0248 0 0.0248 0 -0.0083
a =
1.0000 -3.2632 5.9226 -6.6513 5.0802 -2.3909 0.6307
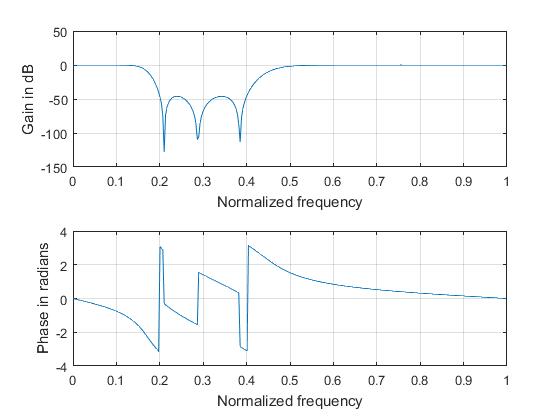
Chebyshev Type II Bandstop Filter
%% To design a Chebyshev 2 bandstop filter for the specifications
alphap = 2; %Pass band attenuation in dB
alphas = 20; %Stop band attenuation in dB
ws = [.2*pi,.4*pi]; %Stop band frequency in radians
wp = [.1*pi,.5*pi]; %Pass band frequency in radians
%To find cutoff frequency and order of the filter
[n,wn] = cheb2ord(wp/pi,ws/pi,alphap,alphas);
%System function of the filter
[b,a] = cheby2(n,alphas,wn,'stop')
w = 0:.01:pi;
[h,ph] = freqz(b,a,w);
m = 20*log(abs(h));
an = angle(h);
subplot(2,1,1); plot(ph/pi,m); grid; xlabel('Normalized frequency'); ylabel('Gain in dB');
subplot(2,1,2); plot(ph/pi,an); grid; xlabel('Normalized frequency'); ylabel('Phase in radians');
Command Window output:
b =
0.4870 -1.7177 3.3867 -4.1110 3.3867 -1.7177 0.4870
a =
1.0000 -2.7289 4.0090 -3.7876 2.5028 -1.0299 0.2357
Conversion of an Analog Filter into a Digital Filter using Impulse Invariance Method
This is a direct implementation of the impinvar function.
%% To convert the analog filter into digital filter using impulse invariance
b = [1,2]; % Numerator coefficients of analog filter
a = [1,5,11,15]; % Denominator coefficients of analog filter
f = 5; % Sampling frequency
[bz,az] = impinvar(b,a,f)
Command Window output:
bz =
0.0000 0.0290 -0.0195
az =
1.0000 -2.0570 1.4980 -0.3679
Conversion of an Analog Filter into a Digital Filter using Bilinear Transformation
bilinear here.
%% To convert the analog filter into digital filter using bilinear transformation
b = [2]; % Numerator coefficients of analog filter
a = [1,3,2]; % Denominator coefficients of analog filter
f = 1; % Sampling frequency
[bz,az] = bilinear(b,a,f)
Command Window output:
bz =
0.1667 0.3333 0.1667
az =
1.0000 -0.3333 0.0000
This repo contains all the scripts used in this post. Here is a link to the previous part, a link to the next part and a link to the references part.
